OpenFst Quick Tour
Below is a brief tutorial on the OpenFst library. After reading this, you may wish to browse the Advanced Usage topic for greater detail, read the library Conventions topic to ensure correct usage and read the Efficiency topic for to ensure efficient usage.Finding and Using the Library
The OpenFst library is a C++ template library. From C++, include<fst/fstlib.h> in the installation include directory and link to libfst.so in the installation library directory. (You may instead use just those include files for
the classes and functions that you will need.) All classes and functions are in the fst namespace; the examples below assume you are within that namespace for brevity. (Include <fst/fst-decl.h> if forward declaration of the public OpenFst
classes is needed.)
As an alternative interface, there are shell-level commands in the installation bin directory that operate on file representations of FSTs.
The command-line flag --help will give usage information.
Example FST
The following picture depicts a finite state transducer: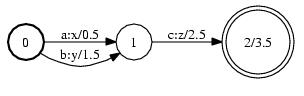 The initial state is label 0. There can only be one initial state.
The final state is 2 with final weight of 3.5. Any state with non-infinite
final weight is a final state. There is an arc (or transition)
from state 0 to 1 with input label
The initial state is label 0. There can only be one initial state.
The final state is 2 with final weight of 3.5. Any state with non-infinite
final weight is a final state. There is an arc (or transition)
from state 0 to 1 with input label a, output label x, and weight 0.5. This FST transduces,
for instance, the string ac to xz with weight 6.5 (the sum of the arc and final weights).
Note we have assumed the library default Weight type for this description.
Creating FSTs
FSTs can be created with constructors and mutators from C++ or from text files at the shell-level. We will show how to create the above example FST both ways.Creating FSTs Using Constructors and Mutators From C++
The following code will create our example FST within C++:// A vector FST is a general mutable FST StdVectorFst fst; // Adds state 0 to the initially empty FST and make it the start state. fst.AddState(); // 1st state will be state 0 (returned by AddState) fst.SetStart(0); // arg is state ID // Adds two arcs exiting state 0. // Arc constructor args: ilabel, olabel, weight, dest state ID. fst.AddArc(0, StdArc(1, 1, 0.5, 1)); // 1st arg is src state ID fst.AddArc(0, StdArc(2, 2, 1.5, 1)); // Adds state 1 and its arc. fst.AddState(); fst.AddArc(1, StdArc(3, 3, 2.5, 2)); // Adds state 2 and set its final weight. fst.AddState(); fst.SetFinal(2, 3.5); // 1st arg is state ID, 2nd arg weightWe can save this FST to a file with:
fst.Write("binary.fst");
Creating FSTs Using Text Files from the Shell
FSTs can be specified using a text file in the AT&T FSM# arc format: src dest ilabel olabel [weight]
# final state format: state [weight]
# lines may occur in any order except initial state must be first line
# unspecified weights default to 0.0 (for the library-default Weight type)
$ cat >text.fst <<EOF
0 1 a x .5
0 1 b y 1.5
1 2 c z 2.5
2 3.5
EOF
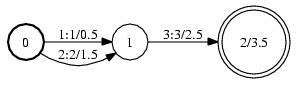
The internal representation of an arc label is an integer.
We must provide the mapping from symbols to integers explicitly with a symbol table file, also in AT&T format:
$ cat >isyms.txt <<EOF <eps> 0 a 1 b 2 c 3 EOF $ cat >osyms.txt <<EOF <eps> 0 x 1 y 2 z 3 EOFYou may use any string for a label; you may use any non-negative integer for a label ID. The zero label ID is reserved for the epsilon label, which is the empty string. We have included 0 in our table, even though it is not used in our example. Since subsequent FST operations might add epsilons, it is good practice to include a symbol for it. This text FST must be converted into a binary FST file before it can be used by the OpenFst library.
# Creates binary Fst from text file. # The symbolic labels will be converted into integers using the symbol table files. $ fstcompile --isymbols=isyms.txt --osymbols=osyms.txt text.fst binary.fst # As above but the symbol tables are stored with the FST. $ fstcompile --isymbols=isyms.txt --osymbols=osyms.txt --keep_isymbols --keep_osymbols text.fst binary.fstIf the labels are represented as non-negative integers in the text FST, then the symbol table files can be omitted. In any case, the internal representation of the FST is:
 Once a binary FST is created, it can be used with the other shell-level programs (on the same machine architecture). It can be loaded inside C++ with:
Once a binary FST is created, it can be used with the other shell-level programs (on the same machine architecture). It can be loaded inside C++ with:
StdFst *fst = StdFst::Read("binary.fst");
(See here for more information on FST I/O.)
Accessing FSTs
FSTs can be examined from C++ accessors or from shell-level commands that read the binary files.Accessing FSTs from C++
Here is the standard representation of an arc:struct StdArc {
typedef int Label;
typedef TropicalWeight Weight; // see "FST Weights" below
typedef int StateId;
Label ilabel;
Label olabel;
Weight weight;
StateId nextstate;
};
Here are some example accesses of an FST:
typedef StdArc::StateId StateId; # Gets the initial state; if == kNoState => empty FST. StateId initial_state = fst.Start(); # Get state i's final weight; if == Weight::Zero() => non-final. Weight weight = fst.Final(i);
# Iterates over the FSTs states.
for (StateIterator<StdFst> siter(fst); !siter.Done(); siter.Next())
StateId state_id = siter.Value();
# Iterates over state i's arcs.
for (ArcIterator<StdFst> aiter(fst, i); !aiter.Done(); aiter.Next())
const StdArc &arc = aiter.Value();
# Iterates over state i's arcs that have input label l (FST must support this -
# in the simplest cases, true when the input labels are sorted).
Matcher<StdFst> matcher(fst, MATCH_INPUT);
matcher.SetState(i);
if (matcher.Find(l))
for (; !matcher.Done(); matcher.Next())
const StdArc &arc = matcher.Value();
More information on state iterators, arc iterators, and matchers are linked here.
There are various conventions that must be observed when accessing FSTs.
Printing, Drawing and Summarizing FSTs from the Shell
The following command will print out an FST in texualt format:# Print FST using symbol table files.
$ fstprint --isymbols=isyms.txt --osymbols=osyms.txt binary.fst text.fst
If the symbol table files are omitted, the FST will be printed with
numeric labels unless the symbol tables are stored with the FST (e.g.,
with fstcompile --keep_isymbols --keep_osymbols).
The following command will draw an FST using Graphviz# Draw FST using symbol table files and Graphviz dot:
$ fstdraw --isymbols=isyms.txt --osymbols=osyms.txt binary.fst binary.dot
$ dot -Tps binary.dot >binary.ps
Summary information about an FST can be obtained with:
$ fstinfo binary.fst fst type vector arc type standard input symbol table isyms.txt output symbol table osyms.txt # of states 3 # of arcs 3 initial state 0 # of final states 1 # of input/output epsilons 0 # of input epsilons 0 # of output epsilons 0 input label multiplicity 1 output label multiplicity 1 # of accessible states 3 # of coaccessible states 3 # of connected states 3 # of connected components 1 # of strongly conn components 3 input matcher y output matcher y input lookahead n output lookahead n expanded y mutable y error n acceptor y input deterministic y output deterministic y input/output epsilons n input epsilons n output epsilons n input label sorted y output label sorted y weighted y cyclic n cyclic at initial state n top sorted y accessible y coaccessible y string n weighted cycles n
FST Operations
Calling FST Operations
The FST operations can be invoked either at the C++ level or from shell-level commands.Calling FST Operations from C++
To invoke FST operations from C++, the FST class hierarchy must first be introduced: The FST interface hierarchy consists of the following abstract class templates:- Fst<Arc>: supports access operations described above
- ExpandedFst<Arc>: an
Fstthat additionally supportsNumStates() - MutableFst<Arc>: an
ExpandedFstthat supports the various mutating operations likeAddStates()andSetStart().
-
VectorFst<Arc>: a general-purpose mutable FST -
ConstFst<Arc>: a general-purpose expanded, immutable FST -
ComposeFst<Arc>: an unexpanded, delayed composition of two FSTs
StdFst is a typedef for Fst<StdArc>. Similar typedefs exist for all the above templates.
For the state and arc iterators, you will get the greatest efficiency if you specify the
most specific FST class as the iterator template argument (e.g., ArcIterator<StdVectorFst> rather
than ArcIterator<StdFst> for a known StdVectorFst).
The C++ FST operations come in three general forms:
- Destructive: When an operation, like
Connect, modifies its input, it has the form:
void Connect(MutableFst<Arc> *fst);
- Constructive: When an operation, like
Reverse, creates a new expanded Fst, it has the form:
void Reverse(const Fst<Arc> &infst, MutableFst<Arc> *outfst);
- Delayed: When an operation, like
ComposeFst, creates a lazy-evaluated Fst, it is a new unexpanded Fst class of the form:
ComposeFst<Arc>(const Fst<Arc> &fst1, const Fst<Arc> &fst2);
Delayed Fsts have constant time-class constructors. When components of delayed Fsts are accessed through the Fst interface, the automaton is built dynamically, just enough to respond to the accesses requested. It is important that the object access conventions are observed for correct operation.
Several operations, like Union, come in more than one of the above forms.
Calling FST Operations from the Shell
The shell-level FST operations typically read one or more input binary FST files, call internally the corresponding C++ operation and then write an output binary FST file. If the output file is omitted, standard output is used. If the input file is also omitted (unary case) or is "-", then standard input is used. Specifically, they have the form:- Unary Operations:
fstunaryop in.fst out.fst
fstunaryop <in.fst >out.fst
- Binary Operations:
fstbinaryop in1.fst in2.fst out.fst
fstbinaryop - in2.fst <in1.fst >out.fst
Example Use: FST Application
One of the most useful finite-state operations is composition, which produces the relational composition of two transductions. It can be used, for example, to apply a transduction to some input:FST Application from C++
#include <fst/fstlib.h>
namespace fst {
// Reads in an input FST.
StdVectorFst *input = StdVectorFst::Read("input.fst");
// Reads in the transduction model.
StdVectorFst *model = StdVectorFst::Read("model.fst");
// The FSTs must be sorted along the dimensions they will be joined.
// In fact, only one needs to be so sorted.
// This could have instead been done for "model.fst" when it was created.
ArcSort(input, StdOLabelCompare());
ArcSort(model, StdILabelCompare());
// Container for composition result.
StdVectorFst result;
// Creates the composed FST.
Compose(*input, *model, &result);
// Just keeps the output labels.
Project(&result, PROJECT_OUTPUT);
// Writes the result FST to a file.
result.Write("result.fst");
}
FST Application from the Shell
# The FSTs must be sorted along the dimensions they will be joined. # In fact, only one needs to be so sorted. # This could have instead been done for "model.fst" when it was created. $ fstarcsort --sort_type=olabel input.fst input_sorted.fst $ fstarcsort --sort_type=ilabel model.fst model_sorted.fst # Creates the composed FST. $ fstcompose input_sorted.fst model_sorted.fst comp.fst # Just keeps the output label $ fstproject --project_output comp.fst result.fst # Do it all in a single command line. $ fstarcsort --sort_type=ilabel model.fst | fstcompose input.fst - | fstproject --project_output result.fst
Available FST Operations
Click on operation name for additional information.| Operation | Usage | Description |
|---|---|---|
| ArcMap | ArcMap(&A, mapper); | transforms arcs in an FST |
| ArcMap(A, &B, mapper); | ||
| ArcMapFst<InArc, OutArc, ArcMapper>(A, mapper); | ||
| fstmap [--delta=$d] [--map=$type] [--weight=$w] in.fst out.fst | ||
| ArcSort | ArcSort(&A, compare); | sorts arcs using compare function object |
| ArcSortFst<Arc, Compare>(A, compare); | ||
| fstarcsort [--sort_type=$type] in.fst out.fst | ||
| Closure | Closure(&A, type); | A* = {ε} ∪ A ∪ AA ∪ .... |
| ClosureFst<Arc>(A, type); | ||
| fstclosure in.fst out.fst | ||
| Compose | Compose(A, B, &C); | composition of binary relations A and B |
| ComposeFst<Arc>(A, B); | ||
| fstcompose a.fst b.fst out.fst | ||
| Concat | Concat(&A, B); | contains the strings in A followed by B |
| Concat(A, &B); | ||
| ConcatFst<Arc>(A,B); | ||
| fstconcat a.fst b.fst out.fst | ||
| Connect | Connect(&A); | removes states and arcs not on a path from the start to a final state |
| fstconnect in.fst out.fst | ||
| Decode | Decode(&A, encoder); | decodes previously encoded Fst |
| DecodeFst(A, encoder); | ||
| fstencode --decode in.fst encoder out.fst | ||
| Determinize | Determinize(A, &B); | creates equiv. FST with no state with two arcs with the same input label |
| DeterminizeFst<Arc>(A); | ||
| fstdeterminize in.fst out.fst | ||
| Difference | Difference(A, B, &C); | contains strings in A but not B; B unweighted |
| DifferenceFst<Arc>(A, B); | ||
| fstdifference a.fsa b.dfa out.fsa | ||
| Disambiguate | Disambiguate(A, &B); | creates equiv. FST with no two successful paths with the same input labels |
| fstdisambiguate in.fst out.fst | ||
| Encode | Encode(&A, encoder); | combines input labels with output labels and/or weights into new input labels |
| EncodeFst(A, encoder); | ||
| fstencode [--encode_labels] [--encode_weights] in.fst encoder out.fst | ||
| EpsNormalize | EpsNormalize(A, &B, type); | creates equiv. FST with any input (output) epsilons at path ends |
| fstepsnormalize [--eps_norm_output] in.fst out.fst | ||
| Equal | Equal(A, B) | determines if FSTs A and B have the same states and transitions with the same numbering and order |
| fstequal a.fst b.fst | ||
| Equivalent | Equivalent(A, B) | determines if acceptors A and B accept the same strings with the same weights |
| fstequivalent a.dfa b.dfa | ||
| Intersect | Intersect(A, B, &C); | contains strings both in A and B |
| IntersectFst<Arc>(A, B); | ||
| fstintersect a.fsa b.fsa out.fsa | ||
| Invert | Invert(&A); | inverse binary relation; exchanges input and output labels |
| InvertFst<Arc>(A); | ||
| fstinvert in.fst out.fst | ||
| Isomorphic | Isomorphic(A, B) | determines if FSTs A and B have the same states and transitions irrespective of numbering and order |
| fstisomorphic a.fst b.fst | ||
| Minimize | Minimize(&A); | transforms to equiv. deterministic FSA with fewest states and arcs |
| Minimize(&A, &B); | transforms to equiv. deterministic FST with fewest states and arcs | |
| fstminimize in.fst out1.fst [out2.fst] | ||
| Project | Project(&A, type); | creates acceptor of just the input or output strings |
| ProjectFst<Arc>(A, type); | ||
| fstproject [--project_output] in.fst out.fsa | ||
| Prune | Prune(&A, threshold); | removes paths outside a threshold of best path |
| fstprune [--weight=$w] in.fst out.fst | ||
| Push | Push<Arc, Type>(&A, flags); | creates equiv. FST pushing weights and/or output labels toward initial or final states |
| fstpush [--push_labels] [--push_weights] [--to_final] in.fst out.fst | ||
| RandEquivalent | RandEquivalent(A, B, npath); | checks if transducers A and B transduce the same randomly-generated string pairs with the same weights |
| fstequivalent --random [-npath=$n] a.fst b.fst | ||
| RandGen | RandGen(A, &B [, opts]); | generates random path(s) through an FST |
| fstrandgen [--max_length=$l] [--npath=$n] [--seed=$s] [--select=$sel] in.fst out.fst | ||
| Relabel | Relabel(&A, isyms, osyms); | changes input and output label IDs |
| RelabelFst<Arc>(A, isyms, osyms); | ||
| fstrelabel [--relabel_isymbols=$isyms] [--relabel_osymbols=$osyms] in.fst out.fst | ||
| Replace | Replace(fst_label_pairs, &B, root_label); | replaces non-terminals with FSTs analogous to an RTN |
| ReplaceFst<Arc>(fst_label_pairs, root_label); | ||
| fstreplace root.fst rootlabel [rule1.fst rule1.label ...] out.fst | ||
| Reverse | Reverse(A, &B); | contains the reversed strings in A |
| fstreverse a.fst out.fst | ||
| Reweight | Reweight(&A, potentials, type); | creates equiv. FST changing arc weights based on potentials |
| fstreweight [--to_final] in.fst potentials.txt out.fst | ||
| RmEpsilon | RmEpsilon(&A); | creates equiv. FST with no input/output epsilons |
| RmEpsilonFst<Arc>(A); | ||
| fstrmepsilon in.fst out.fst | ||
| ShortestDistance | ShortestDistance(A, &distance); | shortest distance from initial state to each state |
| ShortestDistance(A, &distance, true); | shortest distance from each state to final states | |
| fstshortestdistance [--reverse] in.fst [distance.txt] | ||
| ShortestPath | ShortestPath(A, &B, nshortest=1); | N-best paths |
| fstshortestpath [--nshortest=$n] in.fst out.fst | ||
| StateMap | StateMap(&A, mapper); | transforms states in an FST |
| StateMap(A, &B, mapper); | ||
| StateMapFst<InArc, OutArc, StateMapper>(A, mapper); | ||
| fstmap [--map=$type] in.fst out.fst | ||
| Synchronize | Synchronize(A, &B); | synchronizes an FST |
| SynchronizeFst<Arc>(A); | ||
| fstsynchronize in.fst out.fst | ||
| TopSort | TopSort(&A); | sorts an acyclic FST so that all transitions are from lower to higher state IDs |
| fsttopsort in.fst out.fst | ||
| Union | Union(&A, B); | contains strings in A or B |
| UnionFst<Arc>(A, B); | ||
| fstunion a.fst b.fst out.fst | ||
| Verify | Verify(A); | tests sanity of FST's contents |
FST Weights
An arc weight in an FST gives the cost of taking that transition. The OpenFst library supports multiple types of weights -- in fact, any C++ class that meets various properties can be used as theWeight type specified in the Arc template parameter of an Fst.
Several Weight types are predefined in the library that will normally meet your needs.
Among a weight's properties, it must have associated binary operations ⊕ and ⊗ and elements
0 and 1. These are
implemented by a Weight type with functions Plus(x, y) and Times(x, y) and static member functions Zero() and One(), respectively. These must form a semiring; see here for a further description of the constraints on these operations and other properties of weights. ⊕
is used to combine the weight of two identically labeled alternative paths, while ⊗ is used to combine weights along a path or when matching
paths in composition or intersection. A state is final if and only its final weight is not equal to 0 . A transition with weight 1 is, in essence, "free". A path with weight 0 is not allowed (since such paths present technical problems with some algorithms).
The following are some useful weight types:
| Name | Set | ⊕ (Plus) |
⊗ (Times) |
0 (Zero) |
1 (One) |
|---|---|---|---|---|---|
| Boolean | {0, 1} | ∨ | ∧ | 0 | 1 |
| Real | [0, ∞] | + | * | 0 | 1 |
| Log | [-∞, ∞] | -log(e-x + e-y) | + | ∞ | 0 |
| Tropical | [-∞, ∞] | min | + | ∞ | 0 |
min for the Plus operation.
The OpenFst library predefines TropicalWeight  and
and LogWeight  as well as the corresponding
as well as the corresponding
StdArc and LogArc.
These weight classes represent their weight in a single precision float that is a constructor argument. That float
can be directly accessed with member function Value(). For unweighted automata, it
is convenient and customary in this library to use TropicalWeight restricted to Zero() and One().
StdArc is the default arc type for the FST binaries. The Boolean and Real weight types not currently pre-defined.
See here for all pre-defined weight types.
From the shell-level, the FST arc type can be specified to fstcompile with the --arc_type flag; StdArc is the default.
(See here for how to your define your own FST arcs and weights if desired.) | I | Attachment | History | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|---|
| |
numericfst.jpg | r1 | manage | 4.8 K | 2007-06-21 - 21:43 | CyrilAllauzen | |
| |
symbolicfst.jpg | r1 | manage | 4.7 K | 2007-06-21 - 21:43 | CyrilAllauzen |
Topic revision: r113 - 2020-04-25 - MichaelRiley
Ideas, requests, problems regarding TWiki? Send feedback

